보간은 주어진 두 점 사이의 값을 추정하거나, 연속적인 전환을 표현하기 위해 사용됩니다. 보간의 목적은 주어진 데이터나 상태 사이를 부드럽고 자연스럽게 연결하는 것입니다. 이는 수학, 컴퓨터 그래픽, 물리 시뮬레이션, 애니메이션 등
여러 분야에서 중요한 기법입니다.
좀 더 구체적으로 다음과 같이 사용됩니다.
(1) 두 값 사이의 중간 값을 계산하기 위해서
3D애니메이션에서 캐릭터의 키 프레임만 지정해두고,
그 사이 프레임은 보간을 통해 자동으로 생성합니다.
해당 과정에서 선형보간이나 스플라인을 사용하여 연산합니다.
또는 게임 개발에서 시작지점에서 도착지점으로 이동할 때
매 프레임마다의 위치를 계산해야할 때 보간을 사용합니다.
(2) 데이터를 매끄럽게 연결하기 위해
예를들어서 하루 동안 온도를 매 시간마다 측정을 했다라고 생각해보겠습니다.
그걸 시간의 단위로 그래프를 그리려하는데 시간마다 측정했기 때문에
그래프는 이산적으로 표현될 것입니다. 해당 측정한 점들을 기준으로
중간 값들을 예측하여 데이터를 매끄럽게 연결할 수 있습니다.
3) 부드럽고 자연스러운 전환을 위해
Unreal에서 카메라의 시작 위치와 종료 위치만 설정해두면,
그 사이의 경로를 보간 기법(Bezier,Spline등)으로 자연스럽게 이동시킵니다.
이를 통해 회전 및 줌 인 / 아웃을 매끄럽게 연결할 수 있습니다.
4) 최적화와 계산 효율성 :
모든 프레임에 대하여 모델의 위치나 각도 정보를 저장하면 엄청난 메모리가 필요합니다.
대신에 일정 간격의 키 프레임만 저장하고, 키프레임들 사이의 프레임은 보간을 통해
예측하여 메모리를 절약하고 용량을 줄일 수 있습니다.
5) 정확한 시뮬레이션
보간법을 어떤 보간법을 사용하느냐에 따라 데이터의 정확도는 달라지게 됩니다.
예를들어서 점이 5개가 있을 때, 해당 점들의 중간 값을
직선 상에서 중간 값을 구하느냐, 다항식에서의 중간 값을 구하느냐에 따라
그래프는 달라지게 될것입니다.
그 중 오늘은 선형보간법(Lerp)에 대해 알아보겠습니다.
LERP (선형 보간) 은 시작벡터와 종벡터의 사이의 벡터를 추정하는 보간법입니다.

그림에서처럼 P,Q사이의 Ps 벡터에 대한 값을 알아내는 것으로 식은 오른쪽처럼 작성할 수 있습니다.
왜냐하면

시작으로부터 a벡터를 구해 더한다고 생각하면 결국 시점과 종점의 크기를 특정 비율에 따라 Ps를 구하게됩니다.
근데 저에게는 얼마만큼의 비율로 잘라낼 것인가라는 말이 다음과 같이 와닿았습니다.
여기에서 생각에 잠겼는데, 만일 플레이어가 스킬을 사용하면
P지점에서 Q지점으로 가는 로직을 작성하려고할 때 , 해당 LERP 를 사용해 중간 벡터를 구한다고 생각해보겠습니다.
이 중 a벡터란 결국 플레이어의 입장에서 이동하는 벡터와 같다고 생각합니다.
따라서 t의 변화량에 따라 이동하는 거리가 달라질 것이고, 이는 가속도와 연관이 있지 않을까?하는 생각이 들었습니다.
예를들어서 ,
플레이어의 위치 = (1-t)p + t q 에서 t가 커질수록 q에 가까워지게 된다.
그렇다면 "t가 변하는 값이 빠르게 q로 가까워지다가 마지막에 점점 느리게 q로 가까워진다면
위치 변화를 보는 플레이어의 입장에서는 가속도가 붙는것처럼 보이지 않을까?"라는 생각이 들었습니다.
그래서 좀 더 구체적으로 찾아봤습니다.

시간에 따른 t의 값이 선형적이라면 플레이어는 일정한 속도로 목표지점을 향해갈것입니다.
그리고 찾다보니 Ease-In-Out이 있다는 것을 알게 되었습니다.
일반적으로 다항함수의 Ease-In-out을 사용하지만 그렇게되면 추가적인 설정을 하기 어렵습니다.
시간에 따른 t값이 정해져있기 때문입니다.
그래서 지수함수를 이용해서 내가 원하는 강도를 조절할 수 있게 합니다.
언리얼 엔진에서는 Ease-In-Out은 다음과 같은 함수를 사용합니다.
Ease - In )

목표지점으로 갈 때 처음에는 느리게 시작하지만
점점 가속되는 효과를 제공합니다.
주로 시작 부분의 움직임을 부드럽게 만듭니다.
Ease-Out )

움직임이 빠르게 시작하고 점점 감속됩니다.
주로 종료 부분의 움직임을 부드럽게 만듭니다.
Ease-In-Out )
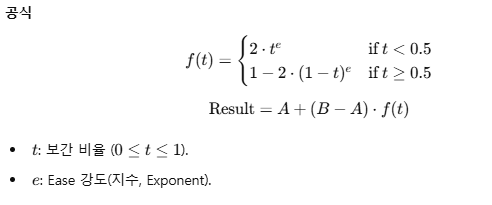
움직임이 느리게 시작(Ease - In)
중간에서 가속
끝에서는 천천히 종료 (Ease-Out)
가장 자연스러운 움직임을 제공합니다.
식에서 보는 것처럼 t값이 0.5에 따라 나뉘기 때문에 Ease-in과 Ease-Out의 식에 2를 곱해준 것을 볼 수 있습니다.
좀 더 시각적으로 비교를 해보면 다음과 같습니다.
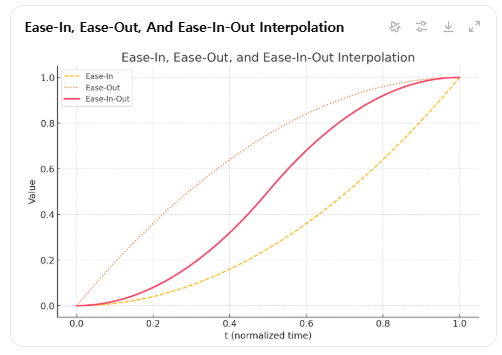
다음은 구면선형보간법(Slerp)에 대해 알아보겠습니다.
'Unreal > Unreal 공부 내용' 카테고리의 다른 글
| GetOverlappingActors(TArray<AActor*> Array) , IsA (0) | 2025.02.09 |
|---|---|
| TSubClassOf , UClass* , StaticClass, 클래스,인스턴스,메타데이터(미완성) (0) | 2025.02.05 |
| Timer(SetTimer...) (0) | 2025.01.24 |
| 구면선형보간법(SLERP) (0) | 2025.01.22 |
| Actor의 생명주기 (라이프 사이클) (1) | 2025.01.21 |